Path Analysis for Software Testing
TLDR; This essay explores the use of graph models in testing and the practice of structural path derivation using 3 coverage concerns: node coverage, link coverage and loop coverage. Predicate coverage is considered but is not covered in detail. An exploration of, and notes on, model path analysis for testing:
Introduction
This text will focus on the structural aspects of model path analysis.
This allows us to learn the basic techniques behind test path derivation. I suspect that most testers will use these techniques intuitively.
Whenever a process is conducted intuitively it always helps to examine it more formally for a number of reasons:
- To allow it to be taught more effectively,
- To explore our understanding of it,
- To apply it consistently.
This text is primarily concerned with an exploration of the understanding of structural path analysis.
The example model
I will use the following model to explore the mechanisms behind path analysis:
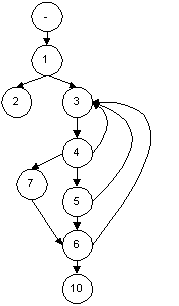
This is undoubtedly a very basic model representation. No tester would ever want to work with a model like the above as it lacks a great deal of semantic information.
Node 4 is either a predicate node or initiates the links to 7, 5 and 3 in parallel. For the purposes of this exploration there are no parallel flows so any node with more than one exit point is a predicate node.
The model does not tell us the predicate conditions under which each link from the predicate node is taken so we work on the assumption that any exit node is equally likely. This makes the loops in the models non-deterministic and limits the strategies which we can apply to the derivation of loop Meta paths.
From this we can see that iterative determinism is not structurally represented but is provided by the semantic information that the model embodies.
Basic Testing approach for Graph Models
Testing Books typically present the reader with the following forms of coverage for flow models.
- Node coverage
- Link coverage
- Loop coverage
Node coverage is achieved when the paths identified hit every node in the graph.
Link coverage is achieved when the paths identified traverse every link in the graph.
Loop coverage is achieved when the numerous paths identified explore the interaction between the sub-paths within a loop. This is a fairly vague description of loop coverage as loop coverage itself is a heuristic technique and will be explored in more detail later in the text.
Pursuing each of these types of coverage leads to path descriptions. Some of the path descriptions are ready to be sensitised and thereby map directly on to a test case. Others are Meta paths and numerous paths can typically be derived from them.
Examples:
- 1 2 is ready to be sensitised.
- *1 [2 [13 4 ]+17 6 ]2 10 is a Meta path and a number of paths can be derived from it:
1 3 4 7 6 101 3 4 3 4 7 6 3 4 7 6 10- etc…
Path 1 2 could be considered a meta path that can only have one path derived from it. Thinking of it in this way may help understanding or the construction of support tools.
Testers who do not do any formal modeling will do this type of path and Meta path identification automatically as it is essentially a form of pattern identification and humans are very good at identifying patterns. We may however miss certain paths or path intricacies and this can lead to defects slipping through the testing process that could have been found by tests within the potential scope of the testing strategies.
The next step, having identified the Meta paths is to apply strategies from them to derive paths:
| Meta Path | Strategy | Path |
|---|---|---|
| 1 [2 [1 3 4 ]*1 7 6 ]*2 10 | => apply ‘once’ to loops => | 1 3 4 7 6 10 |
The strategy-derived paths are then sensitised and tests are identified. For a more detailed treatment of this see Black Box Testing by Boris Beizer.
Node and Link Coverage
Node Coverage can be achieved with the following paths through the model:
- 1 2- 1 3 4 7 6 10- 1 3 4 5 6 10
Link coverage can be achieved with the addition of the path:
- 1 3 4 3 4 5 3 4 5 6 10
We could actually remove node coverage path 3 (- 1 3 4 5 6 10) and replace it with link coverage path 1 leaving us with three paths to derive tests from instead of four but still achieving both node and link coverage.
- 1 2- 1 3 4 7 6 10- 1 3 4 3 4 5 3 4 5 6 10
We will see later that path 3 is actually a derived form of a Loop Meta path. Since at this point we are simply identifying paths for link coverage we will defer the identification of loop paths until later in the text.
Predicate Coverage
Link coverage introduces us to the issue of predicate coverage although the minimal nature of the model makes discussion of this type of coverage more difficult. The following discussion will not fully describe predicate coverage.
The information in the above model obscures the actual conditions associated with the predicate nodes. We do not know the conditions that differentiate the link 4-3, from the links 4-5 and 4-7
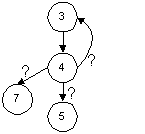
The link 4-3 may be conditional on the evaluation of a compound predicate e.g. when A OR (B AND C). This requires more tests to cover than a simpler predicate e.g. when A, although the path description will be the same for each of the predicate coverage tests e.g.:
3 4 3 4 5[3 4] (When A) 3 4 5[3 4] (When B AND C) 3 4 5- etc. (see below)
We should expand A OR (B AND C) into a truth table to ensure that the link path is not taken under the wrong conditions and also to ensure that we identify all coverage conditions.
| Path ID | A | B | C | Path |
|---|---|---|---|---|
| 1 | T | T | T | 3 4 3 4 5 |
| 2 | T | T | F | 3 4 3 4 5 |
| 3 | T | F | T | 3 4 3 4 5 |
| 4 | T | F | F | 3 4 3 4 5 |
| 5 | F | T | T | 3 4 3 4 5 |
| 6 | F | T | F | 3 4 5 |
| 7 | F | F | T | 3 4 5 |
| 8 | F | F | F | 3 4 5 |
In order to achieve paths 1-5 there has to be a second set of ABC sensitisation values which prevent the loop from being executed again. This is an implementation issue associated with loop test paths.
Predicate Coverage is essentially path sensitisation issue, but it highlights the fact that a strategy aimed at achieving link coverage will provide a weak assurance of the system under test. Of course testers would never construct tests purely on the basis of a link coverage strategy.
Path sensitisation is an important issue that is not covered in this text. (See Beizer)
Loop Coverage

Re-reading the above model we can see it models a sequence of nested loops. The loops are represented by the links from loop exit node 4 to node 3, from 5 to 3 and from 6 to 3.
From our experience as a tester we suspect that achieving link coverage is not enough to assure us that the model has been implemented correctly. Most defect taxonomies will list a variety of defects associated with loops: infinite loops, incorrect exit criteria, etc. (see Testing Computer Software by Kaner et al).
Beizer describes loop testing as a heuristic technique and provides the following coverage strategies:
- Bypass
- Once
- Twice
- Typical
- Max
- Max + 1
- Max - 1
- Min
- Min - 1
- Null
- Negative
Some of these strategies are not applicable for all loops and may lead to the construction of test cases that cannot be executed; this is fine, at least no potential paths have been missed. The scope for testing provided by the model may not represent the scope of testing provided by the system. We will only be able to identify these semantically incorrect paths when we sensitise the paths. Knowledge of these basic strategies allows the tester to be more confident that they are doing the best job that they can.
When analysing loops I generally work with paths using the forms below rather than attempt to follow the graphical representation above.
- 1 2
- 1 [2 [1 3 4 ]*1 7 6 ]*2 10
- 1 [3 [2 [1 3 4 ]*1 5 ]*2 6 ]*3 10
In the path forms above I have assigned each loop a number that represents the sequence of the loop exit node. E.g. loop exit node 4 linking to node 3 is the first loop in the model.
In the model above, the numbering of the loops is less important as each loop links to the same node i.e. node 3 is the loop entry node for all three loops. This statement is only true while the model is represented using paths 2 and 3 above as these only provide link coverage. The numbering of the loops becomes far more important when we consider the representation below, which allows us to go beyond link coverage.
The link coverage paths can be derived directly from the above Meta paths:
- 1 [2[13 4 ]*1 7 6 ]*210
- =>
1 3 4 7 6 10
- =>
- 1 [3[2[13 4 ]*1 5 ]*26 ]*310
- =>
1 3 4 3 4 5 3 4 5 6 10
- =>
If we look at one path (out of many) that we might expect to use during testing:
1 3 4 7 6 3 4 5 6 10
Then we can see that we cannot derive that path from the representations above.
- 1 [3 [2 ( [1 3 4 ]*1 7 )|( [2 [1 3 4 ]*1 5 ]*2)] 6 ]*3 10
The above path can be identified without first constructing an example that disproves the completeness of the link path descriptions. Both of the Meta paths have common elements
- [2 [1 3 4 ]*1…6 ]*2 10
and this suggests that a more complete representation of the Meta path exists.
This form of representation helps to emphasise the different levels of model complexity that have to be considered for each of the coverage concerns.
Beizer’s heuristic strategies are applicable when there is more semantic information in the model than we have. Our model has the minimal amount of information and all the loops are post test loops, we are left with the following path construction strategies.
- Once
- Many
Beizers strategies considered
It is interesting to look at Beizer’s heuristic strategies from a purely structural point of view.
Once
A Path that exercises the loop once would actually be derived during node coverage path analysis, as the loop exit node link is not considered.
1 3 4 5 6 10exercises each loop once.- (23/11/2001) Note: I’m assuming that these are post test loops (Beizer pg71).
Many: Twice, Typical, Max, Max +1, Min, Min -1
I am considering twice, typical, max, max+1, min and min - 1 as instances of the ‘many’ strategy because structurally the loops are non-deterministic and we have no way of knowing how often the loop can be executed.
As a consequence they are all sensitised instances of the paths identified by the ‘many’ strategy.
Bypass, Null, Negative
In order to affect a bypass strategy, structurally, there has to be a structural representation in the model. There is an example of this in the model in the sense that the sub path 4 7 6 represents a bypass of loop exit node 5.
But then this isn’t typically what is meant by a bypass strategy. The bypass strategy is a sensitisation approach to a path that does have a loop representation in it. The bypass strategy refers to a path such as 1 [3 4]* 5 6 10 and asks, is there a way to construct a case which sensitises that path representation in such a way that the path traversed is 1 5 6 10.
This is a sensitisation issue and is a mechanism for forcing testers to think outside the box, the box being the model that we are working with. This strategy encourages us to think, is there anyway that I can make it do what it is not supposed to do. It is very definitely a defect detection strategy.
In effect, this sensitisation strategy, if it can be used to produce a case either points out that our model is wrong and would require an extra link from 1 to 5 (see below), or it would point out that the system under test incorrectly implemented our model.
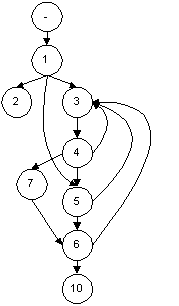
This strategy is interesting because the implications of this strategy do not just apply to loops; they apply to any part of the model. Is there any way to bypass node 7 when moving from node 4 to 6? If there is it implies the existence of a defect in our model or the system.
This strategy is the perfect example of testing thinking, thinking outside the box or constructing structurally ill formed paths. But in order to think outside the box we must know what the box is, hence my laborious presentation of the structural aspects of path analysis.
The skill of testing is to approach the construction of ill formed paths appropriately. But it is entirely possible that these are ill formed paths only because the model is not rich enough to test from. If we had a supplementary model that provided semantic information about the predicate nodes, or the data that is processed, then the combination of these models could result in the construction of structurally ill formed paths that are semantically well formed.
This strategy also highlights the assumptions used when constructing the model. The assumptions are that each link has an equal probability of occurring and that loops are not intrinsic to the model, rather that loops are represented by the links between nodes. Loops are in effect constructed from GOTOs rather than ‘do while’ loops. As a consequence each of my loops is represented by [3 4]* where the * means ‘1 or more times’. If the loops were intrinsic to the model then we could argue the same graph, and the same representation [3 4], but in this case the would mean ‘0 or more times’. This thinking is unlikely to occur in practise as most people will adopt a GOTO perspective when constructing models as this is the most natural way to think about a loop (in a graph) and may be why GOTOs were around before structured loop constructs.
Constructing the graphs and models is outside the scope of this set of notes.
Conclusion
This text has introduced path analysis from a purely structural perspective as this allows a clearer examination of some of the thinking processes and strategies involved in path analysis.
In the real world testing is unlikely ever to be conducted like this as our tests will never be purely structurally based. We have to sensitise paths in order to derive tests. Path sensitisation requires a more semantically rich model or supplementary models that provide the information required to process the model semantically i.e. a set of test conditions, domain analysis, requirements analysis.
The techniques presented here are worth thinking about. They are equally easily mapped on to test script production with the test cases themselves providing the sensitisation information. Using the information presented in this text we can assess the level of coverage achieved on the script model by the test cases compared to the potential coverage.







